Vaccination campaign impact • vaccinationimpact

library(vaccinationimpact)

This package proposes to assess the impact of vaccination campaigns using the following methods:

Number of events averted by vaccination (NAE)
Number of events avertable by increasing the vaccine coverage (NAbE)
Number needed to vaccinate (NNV) to prevent one event

Mathematical Formulas

1. Number of events averted by vaccination (NAE)

The number of events averted by vaccination at time $t$ is calculated as:

$NAE_t = e_{A(t)} \frac{VC_t VE_t}{(1 - VC_t VE_t)}$

with:

$e_{A(t)}$ : Number of events at time $t$
$VE_t$ : Vaccine effectiveness at time $t$
$VC_t$ : Vaccine coverage at time $t$

2. Number of avertable events considering an increase in final coverage (NAbE)

The number of averted events with alpha parameter at time $t$ :

$NAbE_t(\alpha) = e_{A(t)} \frac{VC(\alpha)_t VE_t}{(1 - VC(\alpha)_t VE_t)}$

with:

$e_{A(t)}$ : Number of events at time $t$
$VC(\alpha)_t$ : Hypothetical vaccine coverage during time $t$ if the vaccine coverage was increased by a factor of alpha parameter
$VE_t$ : Vaccine effectiveness at time $t$

$VC(\alpha)_t$ is computed as:

$VC_t(\alpha) = \sum_{i=1}^{t} (VC_t - VC_{t-1}) \left(1 + \frac{\alpha}{VC_T}\right)$

with:

$VC_t$ : Vaccine coverage at time $t$ ( $VC_0 = 0$ )
$VC_{t-1}$ : Vaccine coverage at time $t-1$
$\alpha$ : Increase in final vaccine coverage
$VC_T$ : Maximum vaccine coverage observed

3. Number Needed to Vaccinate (NNV)

Machado et al. method

The number needed to vaccinate at time $t$ is calculated as:

$NNV_t = \frac{1}{R_{B(t)} VE_t}$

where $R_{B(t)} = \frac{e_{A(t)} + NAE_t}{N_t}$ , $R_{B(t)}$ represents the rate of events expected in a counterfactual population without a vaccination program

with:

$VE_t$ : Vaccine effectiveness at time $t$
$e_{A(t)}$ : Number of events at time $t$
$NAE_t$ : Number of events averted by vaccination at time $t$
$N_t$ : Population at risk at time $t$

Tuite and Fisman method

The number needed to vaccinate at time $t$ is calculated as:

$NNV_t = \frac{v_t}{NAE_t}$

with:

$v_t$ : Number of vaccinated individuals at time $t$

Example

We use some toy data to illustrate the usage of the package: weekly coverage, incidence and vaccine effectiveness are provided in the package.

data(coverage_and_incidence_mock_data)
coverage <- coverage_and_incidence_mock_data$coverage_data
incidence <- coverage_and_incidence_mock_data$incidence_data

Coverage data:

The coverage values are computed considering a sample size of 1234 individuals.

head(coverage)
#>         week number_of_vaccinated weekly_coverage cumulative_coverage
#> 1 2023-10-01                   94      0.07617504          0.07617504
#> 2 2023-10-08                  154      0.12479741          0.20097245
#> 3 2023-10-15                  134      0.10858995          0.30956240
#> 4 2023-10-22                  143      0.11588331          0.42544571
#> 5 2023-10-29                  123      0.09967585          0.52512156
#> 6 2023-11-05                   69      0.05591572          0.58103728

Incidence data:

head(incidence)
#>         week events
#> 1 2023-10-01     45
#> 2 2023-10-08     56
#> 3 2023-10-15     48
#> 4 2023-10-22     49
#> 5 2023-10-29     42
#> 6 2023-11-05     35

Vaccine effectiveness data:

data(ve_mock_data)
head(ve_mock_data)
#>         week        ve
#> 1 2023-10-02 0.6344967
#> 2 2023-10-09 0.6493827
#> 3 2023-10-16 0.7369862
#> 4 2023-10-23 0.6604973
#> 5 2023-10-30 0.6610903
#> 6 2023-11-06 0.7377342

NAE

vaccine_effectiveness <- ve_mock_data$ve

nae <- compute_events_averted_by_vaccination(
  number_of_events = incidence$events,
  cumulative_coverage = coverage$cumulative_coverage,
  vaccine_effectiveness = vaccine_effectiveness
)
plot(nae, type = "l", xlab = "Time", ylab = "Events averted")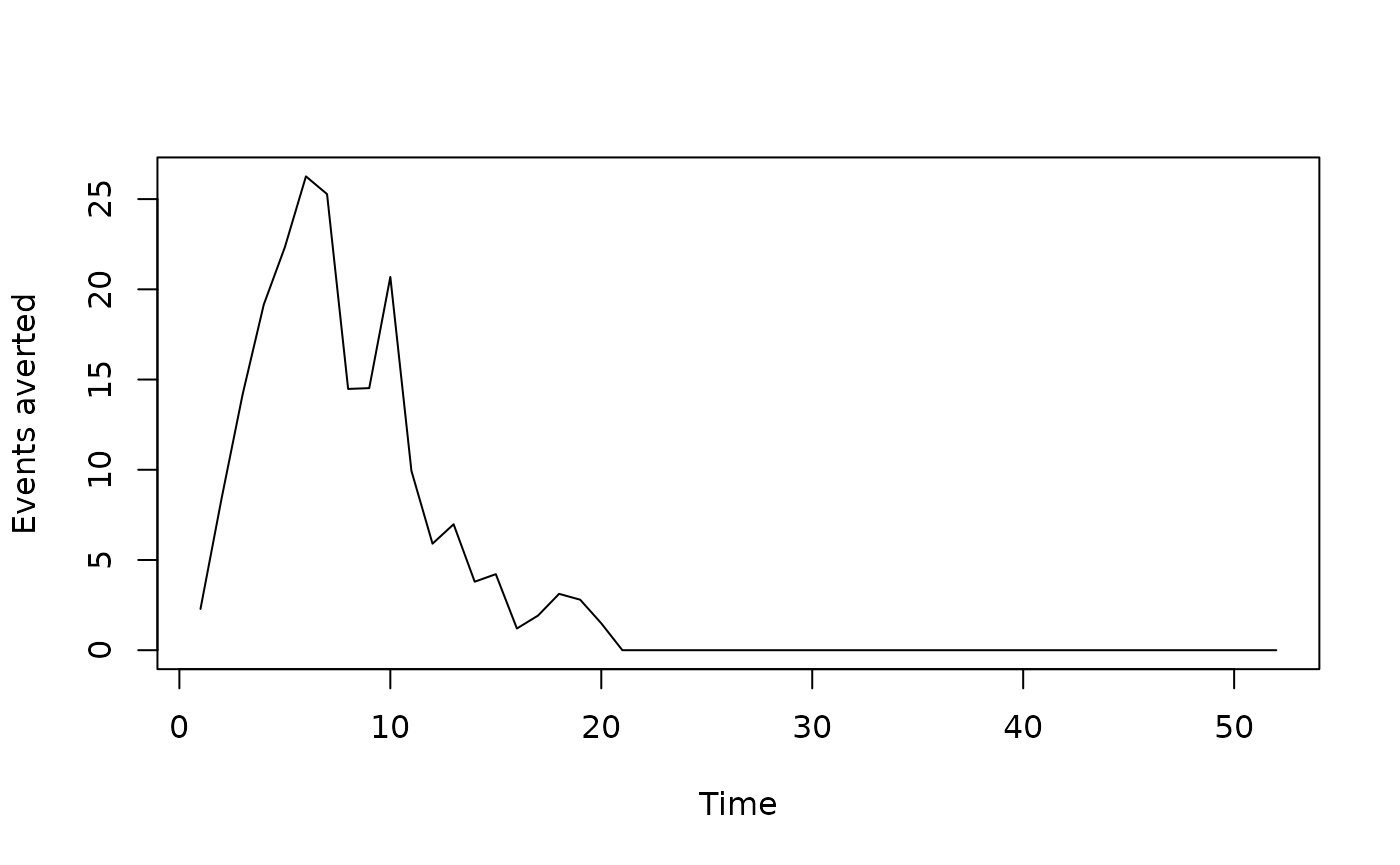

NAbE

nabe <- compute_events_avertable_by_increasing_coverage(
  number_of_events = incidence$events,
  cumulative_coverage = coverage$cumulative_coverage,
  vaccine_coverage_increase = 0.1, # 10% increase in final coverage
  vaccine_effectiveness = vaccine_effectiveness
)

plot(nabe$new_vaccine_coverage, type = "l", xlab = "Time", ylab = "Vaccine coverage with 10% increase")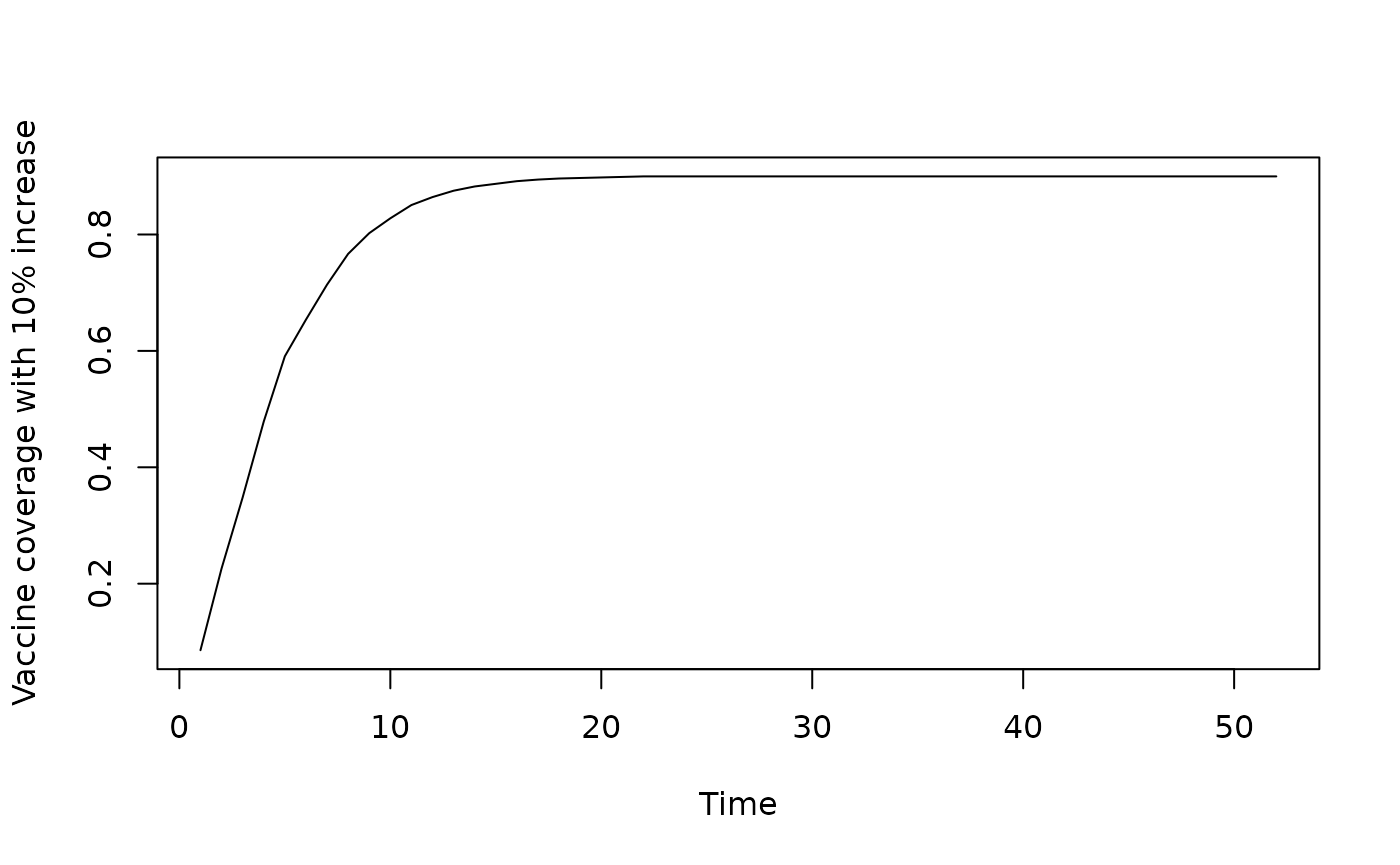

plot(nabe$nabe, type = "l", xlab = "Time", ylab = "Events averted")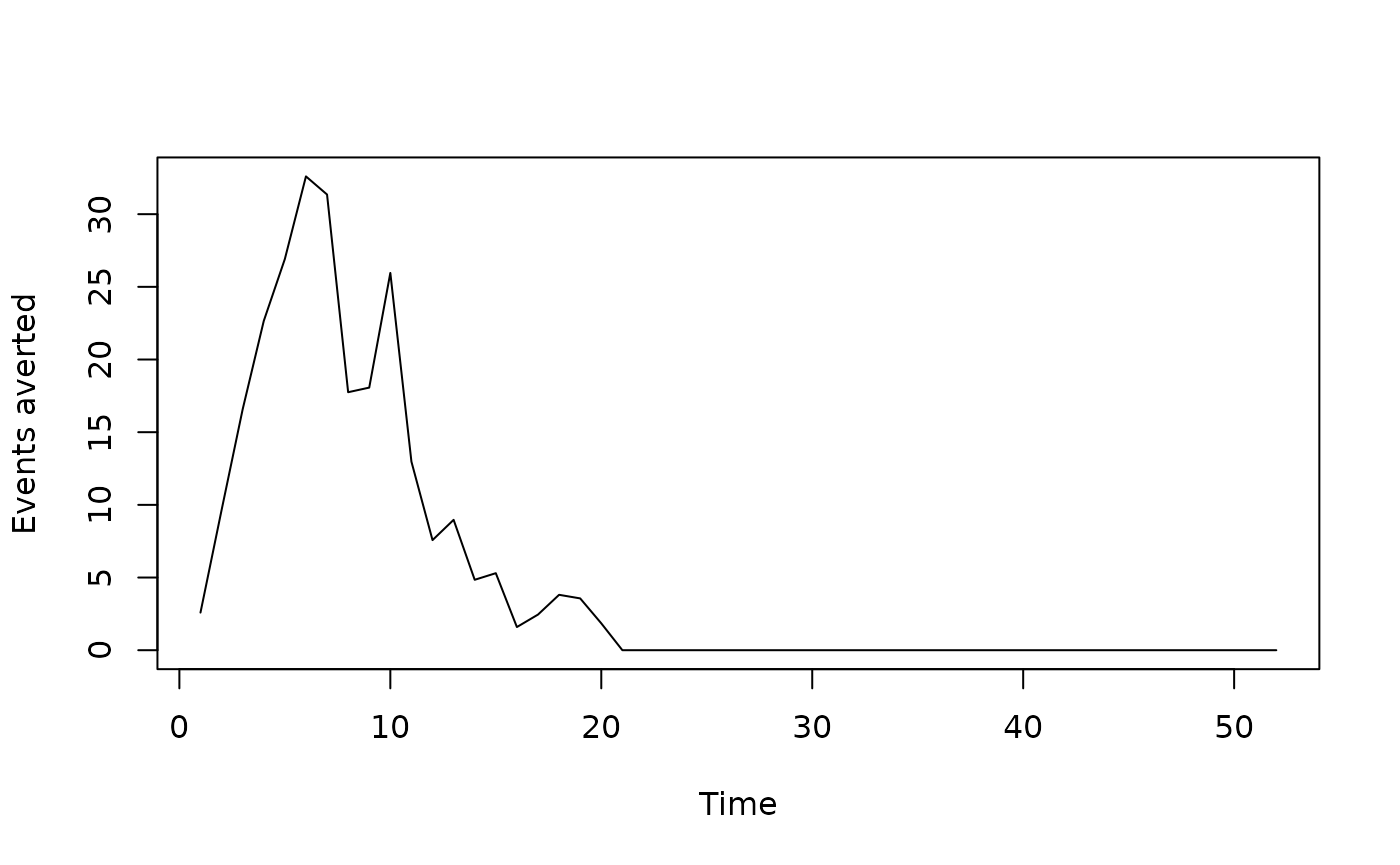

NNV

Machado et al. method

sample_size <- 1234

nnv <- compute_number_needed_to_vaccinate_machado(
  number_of_events = incidence$events,
  number_of_events_averted = nae,
  population_size = sample_size,
  vaccine_effectiveness = vaccine_effectiveness
)
nnv
#>  [1]  41.12997  29.50475  26.92473  27.41407  29.01461  27.30541  30.97586
#>  [8]  58.08314  60.58614  43.89116  93.86294 160.55538 137.54650 255.03374
#> [15] 230.88015 812.75083 511.59870 314.74289 351.58960 661.23225        NA
#> [22]        NA        NA        NA        NA        NA        NA        NA
#> [29]        NA        NA        NA        NA        NA        NA        NA
#> [36]        NA        NA        NA        NA        NA        NA        NA
#> [43]        NA        NA        NA        NA        NA        NA        NA
#> [50]        NA        NA        NA

Tuite and Fisman method

nnv <- compute_number_needed_to_vaccinate_tuite_fisman(
  number_of_vaccinated = cumsum(coverage$number_of_vaccinated),
  number_of_events_averted = nae
)
nnv
#>  [1]  41.12997  29.50475  26.92473  27.41407  29.01461  27.30541  30.97586
#>  [8]  58.08314  60.58614  43.89116  93.86294 160.55538 137.54650 255.03374
#> [15] 230.88015 812.75083 511.59870 314.74289 351.58960 661.23225        NA
#> [22]        NA        NA        NA        NA        NA        NA        NA
#> [29]        NA        NA        NA        NA        NA        NA        NA
#> [36]        NA        NA        NA        NA        NA        NA        NA
#> [43]        NA        NA        NA        NA        NA        NA        NA
#> [50]        NA        NA        NA

References

We applied an adapted version of methods used by Foppa et al. and Machado et al. for influenza vaccination impact.

Foppa IM, Cheng PY, Reynolds SB, Shay DK, Carias C, Bresee JS, et al. Deaths averted by influenza vaccination in the U.S. during the seasons 2005/06 through 2013/14. Vaccine. 2015 June 12;33(26):3003–9.
Machado A, Mazagatos C, Dijkstra F, Kislaya I, Gherasim A, McDonald SA, et al. Impact of influenza vaccination programmes among the elderly population on primary care, Portugal, Spain and the Netherlands: 2015/16 to 2017/18 influenza seasons. Euro Surveill Bull Eur Sur Mal Transm Eur Commun Dis Bull. 2019 Nov;24(45):1900268.
Tuite AR, Fisman DN. Number-needed-to-vaccinate calculations: fallacies associated with exclusion of transmission. Vaccine. 2013 Jan 30;31(6):973-8.